Aula 1 - Introdução à Geração de Energia

Por quê estudar Geração de Energia

Afinal, energia pode ser gerada? Este nome não é estranho?

Você pode entender esta disciplina como o estudo da geração de energia útil - que, em Engenharia Térmica, geralmente significa duas coisas:

1. Calor a altas temperaturas;
2. Potência mecânica.

Calor é útil em processos gerais de aquecimento, como para conforto térmico em regiões muito frias e para diminuir a viscosidade de óleos lubrificantes. Potência mecânica, em geral, sempre é útil para movimentar cargas e gerar energia elétrica - ou, no mínimo, para ser dissipada de volta e gerar calor.

Nesta disciplina, vamos estudar geradores de vapor - equipamentos que produzem vapor d’água a altas pressões e temperatura para movimentar turbinas e alimentar trocadores de calor. O vapor é extensivamente usado como transportador de energia pela sua ampla disponilibidade, atoxicidade e alto calor específico - o que significa que uma pequena massa de vapor absorve ou rejeita energia sem grandes variações de temperatura.

A fonte de calor (que vaporiza a água) é geralmente uma fornalha onde ocorre uma reação de combustão, e este é exclusivamente o foco deste curso.

Máquinas Térmicas e Ciclo de Rankine

Geradores de vapor são geralmente usados em sistemas chamados de máquinas térmicas - ciclos que recebem calor de uma fonte e convertem parte dele em trabalho. Motores de combustão interna são um exemplo clássico de máquina térmica, que funciona à base de gases de combustão. Usinas termelétricas são máquinas térmicas que funcionam com vapor.

Na realidade, geradores de vapor não precisam ser utilizados em máquinas térmicas, e é possível simplesmente ter uma fornalha que recebe água de uma fonte contínua (como um rio), é constantemente alimentada com ar e combustível (usando automação industrial), e gera vapor para um sistema de aquecimento residencial, por exemplo, sem nenhuma turbina envolvida. Entretanto, isto é um desperdício: a fornalha atinge temperaturas acima de 1000 ºC, e trocadores de calor dificilmente trabalham acima dos 200 ºC, até pela resistência dos materiais que compõem o trocador, enquanto que turbinas trabalham perto dos 500 ºC. Assim, faz mais sentido, se vamos ter uma reação de combustão, usar o vapor quente para uma turbina e, após ele expandir e se resfriar um pouco, passar pelos trocadores de calor conforme desejado.

O ciclo termodinâmico básico para geradores de vapor é o ciclo de Rankine. A figura abaixo mostra um diagrama temperatura-entropia do ciclo Rankine simples:

O ciclo 1-2-3-4-a-1 representa uma versão idealizada do ciclo, onde a turbina 1-2 trabalha na região bifásica, o que é impossível com as tecnologias atuais. O ciclo com superaquecimento 1'-2'-3-4-a-1' é bem mais realista. Porém, como vamos ver, a caldeira, o trocador de calor que recebe energia da fornalha e onde acontece o processo 4-a-1, é um equipamento bem diferente do superaquecedor, onde acontece o processo 1-1'. Assim, o ciclo sem superaquecimento pode ser útil para concentrar as atenções na caldeira e geração de vapor saturado.

Usualmente, na análise de ciclos de potência a vapor, desprezam-se variações de energia cinética e potencial entre a entrada e saída dos equipamentos. Como os processos isotérmicos são sempre isobáricos (é como conseguimos que os processos de escoamento sejam isotérmicos), nesses trechos não há realização de trabalho (que modifique a pressão). Nos processos isentrópicos, não há transferência de calor. Assim, em cada processo, a troca de calor ou de trabalho pode ser expressa como uma variação de entalpias.

Para esse caso, o calor que entra no ciclo é, por unidade de vazão de vapor que escoa na caldeira, é:

$$ q_{\mathrm{cald}} = h_1 - h_4 $$

onde

$$ h_1 = h_v(P_{\mathrm{cald}}) $$

onde o ciclo é geralmente especificado em termos de uma pressão de caldeira \(P_{\mathrm{cald}} = P_1 = P_a = P_4\) e uma pressão de condensador \(P_{\mathrm{cond}} = P_3 = P_2\). Nestes textos, o índice \(v\) representa o estado de vapor saturado, e \(l\) o estado de líquido saturado.

Para o estado 4, primeiro achamos o estado 3:

$$ h_3 = h_l (P_{\mathrm{cond}}) $$

e, para o processo 3-4, que representa um bombeamento isentrópico de um fluido incompressível, podemos usar a expressão:

$$ h_4 - h_3 = w_{\mathrm{bomba}} = v_3 (P_{\mathrm{cald}} - P_{\mathrm{cond}}) $$

O calor (positivo) rejeitado no condensador é:

$$ q_{\mathrm{cond}} = h_2 - h_3 $$

onde

$$ h_2 = h(P_{\mathrm{cond}},s = s_1 = s_v(P_{\mathrm{cald}})) $$

Alternativamente, podemos calcular com base no título do ponto 2:

$$ x_2 = \frac{h_2 - h_l(P_{\mathrm{cond}})}{h_v(P_{\mathrm{cond}}) - h_l(P_{\mathrm{cond}})} = \frac{s_2 - h_l(P_{\mathrm{cond}})}{s_v(P_{\mathrm{cond}}) - s_l(P_{\mathrm{cond}})} $$

observando que, pelo processo ser isentrópico, \(s_2 = s_1\). As equações acima podem ser resolvidos interpolando em tabelas ou usando ferramentas computacionais, como será mostrado posteriormente.

O trabalho líquido é \(w_{\mathrm{liq,sai}} = q_{\mathrm{cald}} - q_{\mathrm{cond}}\), e a eficiência térmica é \(\eta_{\mathrm{t}} = \frac{w_{\mathrm{liq,sai}}}{q_{\mathrm{cald}}}\).

Irreversibilidades

A EPE publica frequentemente relatórios sobre o uso de energia no Brasil.

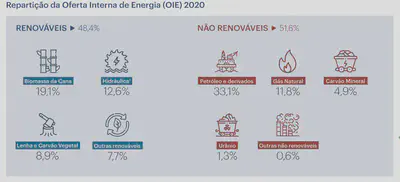
Como você pode ver acima, grande parte da energia gerada é através de usinas termelétricas e processos de geração de vapor. Biomassa, carvão mineral, lenha, gás natural, alguns derivados de petróleo - a principal aplicação destes combustíveis é em geradores de vapor.

O problema é que os processos de geração de vapor e de aplicação do Ciclo Rankine estão associados com várias perdas:

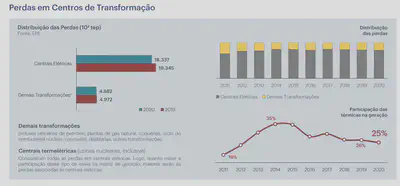
É impossível ter um ciclo termodinâmico com eficiência de 100% - isto é o Enunciado de Kelvin-Planck da Segunda Lei da Termodinâmica. Usinas hidrelétricas, por exemplo, não seguem ciclos termodinâmicos e portanto podem ter eficiências muito altas. Como está colocado acima, quanto mais as termelétricas são usadas, menores as eficiências e maiores as perdas (i.e., mais combustível é queimado que não gera energia útil).

As perdas de uma usina a vapor seriam minimizadas se ela seguisse o Ciclo de Carnot de vapor, uma modificação do ciclo tradicional de Carnot de pistão, mas que usa máquinas de fluxo:

cujo diagrama \(T-s\) é:

Por quê não podemos usar o ciclo de Carnot em processos de geração de vapor?

Em primeiro lugar, para manter os processos isotérmicos dentro do domo de saturação, os processos isentrópicos de compressão e expansão são agora bifásicos - o que, novamente, é bastante difícil de fazer na prática.

Em segundo lugar, este ciclo não gera tanta potência quanto poderia. Compare:

O ciclo de Carnot é mais eficiente que os dois (por quê?), mas o ciclo de Rankine é mais potente (por quê?)

O gargalo de eficiências, a fonte de irreversibilidades, é a transferência de calor. O problema de engenharia, e o que vamos estudar profundidade, é como aproveitar o máximo de energia dos gases quentes.

Exemplos

Neste estágio do curso, é importante saber fazer uma Análise de Primeira Lei da Termodinâmica nos dois ciclos descritos acima (Carnot e Rankine simples). Eu recomendo usar CoolProp para calcular os pontos termodinâmicos.

Comparação de ciclos de Carnot e Rankine simples

Exercício 10.25 [2]: Os trabalhos líquidos e as eficiências térmicas do ciclo de Carnot e do ciclo de Rankine simples ideal devem ser calculados e comparados. Em ambos os casos o vapor de água entra na turbina a 5MPa como vapor saturado, e a pressão no condensador é de 50 kPa. No ciclo de Rankine, o estado na saída do condensador é líquido saturado e, no ciclo de Carnot, o estado na entrada na caldeira é líquido saturado. Analise a influência da pressão de caldeira nesses parâmetros.

from CoolProp.CoolProp import PropsSI

Pcond = 50e3
Pcald = 5e6

# 4' = entrada da caldeira de Carnot
# 1 = entrada da turbina
h4l = PropsSI("H","P",Pcald,"Q",0,"Water")
h1 = PropsSI("H","P",Pcald,"Q",1,"Water")

Tcald = PropsSI("T","P",Pcald,"Q",0,"Water")
Tcond = PropsSI("T","P",Pcond,"Q",0,"Water")

eta_Carnot = 1 - Tcond/Tcald
print("Eficiência de Carnot: %.2f %%" %(eta_Carnot*100))

## Eficiência de Carnot: 34.00 %

qcald_Carnot = h1 - h4l
w_Carnot = qcald_Carnot * eta_Carnot
print("Trabalho de Carnot: %.2f kJ/kg" %(w_Carnot/1000))

# 3 = saída do condensador de Rankine

## Trabalho de Carnot: 557.49 kJ/kg

h3 = PropsSI("H","P",Pcond,"Q",0,"Water")
v3 = 1/PropsSI("D","P",Pcond,"Q",0,"Water")

wbomba = v3 * (Pcald - Pcond)
h4 = h3 + wbomba

qcald_Rankine = h1-h4

# 2 = entrada do condensador de Rankine
s1 = PropsSI("S","P",Pcald,"Q",1,"Water")
s2 = s1
h2 = PropsSI("H","P",Pcond,"S",s2,"Water")

qcond_Rankine = h2 - h3

w_Rankine = qcald_Rankine - qcond_Rankine
eta_Rankine = w_Rankine/qcald_Rankine
print("Eficiência de Rankine: %.2f %%" %(eta_Rankine*100))

## Eficiência de Rankine: 29.32 %

print("Trabalho de Rankine: %.2f kJ/kg" %(w_Rankine/1000))

## Trabalho de Rankine: 717.89 kJ/kg

Referências

[1]: Moran, Michael J; Shapiro, Howard N. Fundamentals of Engineering Thermodynamics (5 ed.). Chichester: Wiley, 2006.

[2]: Çengel, Y. A., & Boles, M. A. Termodinâmica (7 ed.). Porto Alegre: AMGH, 2013.

[3] Sonntag, R. E; Borgnakke, C.; Van Wylen, G. J. Fundamentos da Termodinâmica (6a ed.). São Paulo: Edgard Blücher, 2003.