Aula 7 - Tubos capilares

Vazão de compressores

Um compressor succiona vapor do evaporador e o comprime até a pressão de condensação, como já visto.

Vamos considerar para esta aula que segue um compressor alternativo ideal (isentrópico) monocilindro de simples efeito com volume morto, com cilindrada \(\mathcal{V}_{\mathrm{D}}\) e fração de volume morto (em relação à cilindrada) \(\varepsilon\), que funciona em uma rotação fixa \(n\).

Seja 1 o estado de sucção do compressor, possivelmente superaquecido. A vazão do compressor pode então ser calculada como:

$$ \dot{m} = \frac{\mathcal{V} _{\mathrm{D}}n}{v _1}\left(1 + \varepsilon\left(1-\frac{v _{\mathrm{1}}}{v (P = P _{\mathrm{cond}},s=s1)}\right)\right) $$

No caso particular onde o estado de sucção não tem superaquecimento, a vazão acima depende apenas das temperaturas de evaporação e condensação:

$$ \dot{m} = \frac{\mathcal{V} _{\mathrm{D}}n}{v _v(t _{\mathrm{evap}})}\left(1 + \varepsilon\left(1-\frac{v _v(t _{\mathrm{evap}})}{v (P = P _{\mathrm{sat}}(t _{\mathrm{cond}}),s=s_v(t _{\mathrm{evap}}))}\right)\right) $$

Como vimos anteriormente, as condições de operação em um sistema de refrigeração real mudam, e geralmente mudam no lado de evaporação, pela mudança na carga térmica. Portanto, é interessante analisar a vazão de um compressor de geometria e rotação fixas, a uma temperatura de condensação (ambiente) constante, conforme a temperatura de evaporação muda (novamente, assumindo sucção de vapor saturado):

import numpy as np
from CoolProp.CoolProp import PropsSI
import matplotlib.pyplot as plt
import pandas as pd

plt.rc('font', size=12)


fluid = 'R134a'

t_evap_values = np.linspace(-20,5)
t_cond_values = np.linspace(35,55)

Vd = 13.54e-6 # in m3
n = 60 #Hz
epsilon = 5e-2

V_dot = Vd*n

def m_dot_compressor_fun(t_evap,t_cond):
  v1 = 1.0/PropsSI("D","T",t_evap+273,"Q",1,fluid)
  s1 = PropsSI("S","T",t_evap+273,"Q",1,fluid)
  P_cond = PropsSI("P","T",t_cond+273,"Q",1,fluid)
  v2 = 1.0/PropsSI("D","S",s1,"P",P_cond,fluid) 
  
  eta_v = 1 - epsilon*(1 - v1/v2)
  m_dot_compressor = V_dot*eta_v/v1
  return m_dot_compressor

# stolen from https://www.delftstack.com/howto/numpy/python-numpy-combinations/#:~:text=We%20can%20also%20use%20the%20meshgrid%20%28%29%20function,and%20returns%20the%20cross-product%20of%20the%20two%20arrays.
X = np.array(np.meshgrid(t_evap_values, t_cond_values)).T.reshape(-1,2)

m_dot_compressor_values = np.array([
  m_dot_compressor_fun(t_evap,t_cond) for (t_evap,t_cond) in X
])

compressor_df = pd.DataFrame(
  {'t_evap[C]': X[:,0],
  't_cond[C]': X[:,1],
  'm_dot[kg/s]': m_dot_compressor_values}
)


t_cond = t_cond_values[-1]
t_evap_tc = compressor_df[compressor_df['t_cond[C]'] == t_cond]['t_evap[C]'].values
m_dot_compressor_tc = compressor_df[compressor_df['t_cond[C]'] == t_cond]['m_dot[kg/s]'].values

fig, ax = plt.subplots()
ax.plot(t_evap_tc,m_dot_compressor_tc*3600,'ko',label='Temp. cond. = %.2f ºC' %(t_cond,))
ax.grid()
ax.legend()
ax.set_xlabel("Temperatura de evaporação [ºC]")
ax.set_ylabel("Vazão mássica [kg/h]")
plt.show()

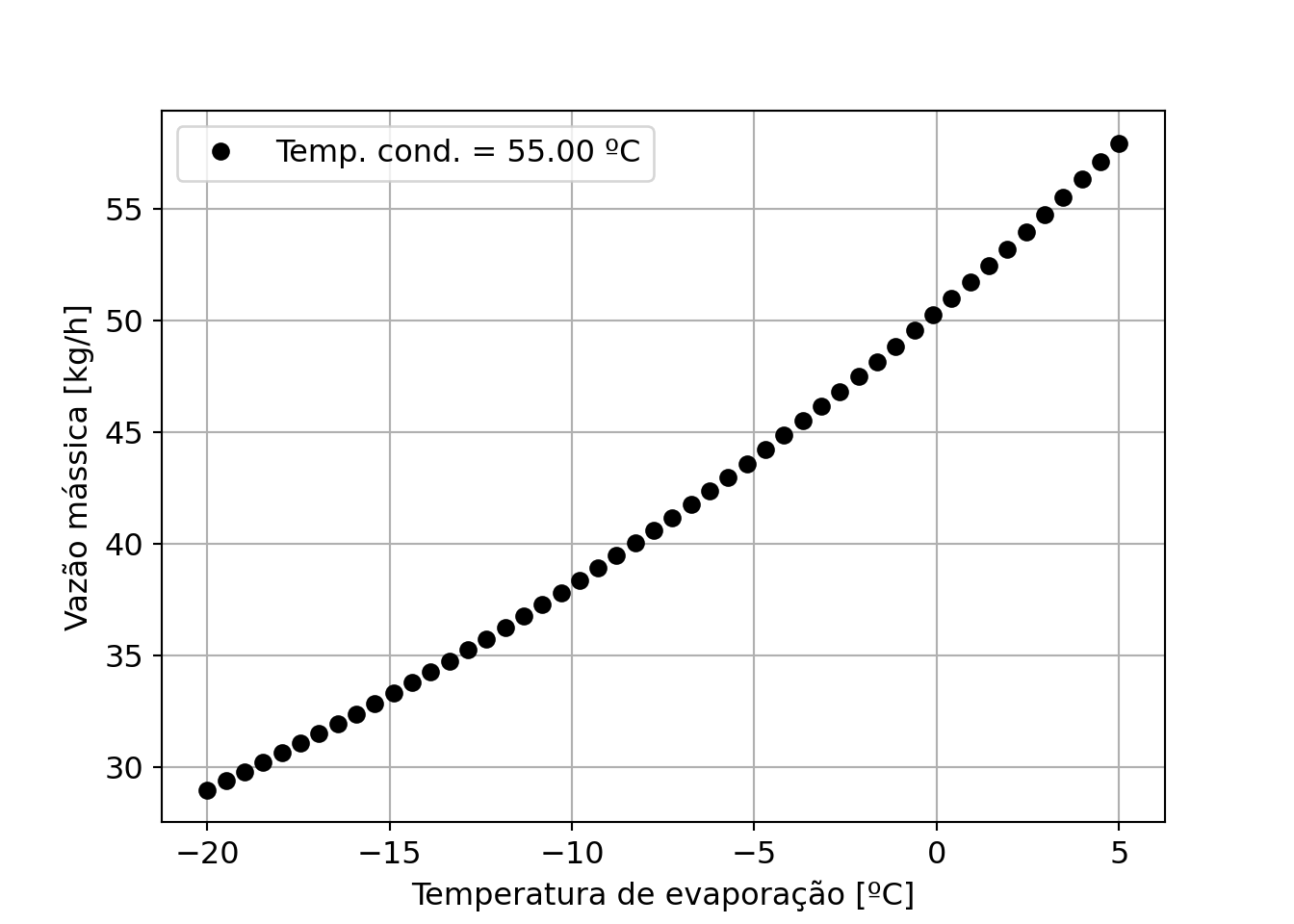O que está acontecendo com essa curva:

1. Como a temperatura de evaporação pode subir? (use os conceitos de trocadores de calor)
2. Por que a vazão de um compressor sobe com a temperatura de evaporação?

Ajuste polinomial na vazão de compressores

Podemos tentar ajustar uma curva quadrática a este comportamento:

$$ \dot{m} _{\mathrm{comp}} = a _0 + a _1 t _{\mathrm{evap}} + a _2 t _{\mathrm{evap}}^2 $$

Em termos estatísticos, isso equivale a dizer que, para cada valor \(t_{\mathrm{evap},i}\) e sua correspondente vazão \(\dot{m}_{\mathrm{comp},i}\), existem constantes \(a_j\) tal que

$$ \dot{m} _{\mathrm{comp},i} = a _0 + a _1 t _{\mathrm{evap},i} + a _2 t _{\mathrm{evap},i}^2 + e_i $$

onde \(e_i\) é um termo de erro, que queremos que seja o menor possível:

$$ \begin{split} e_i = & \left(\frac{\mathcal{V}_{\mathrm{D}}n}{v_v(t_{\mathrm{evap},i})}\left(1 + \varepsilon\left(1-\frac{v_v(t_{\mathrm{evap},i})}{v (P = P_{\mathrm{sat}}(t_{\mathrm{cond}}),s=s_v(t_{\mathrm{evap},i}))}\right)\right)\right)- \\ & \left(a _0 + a _1 t _{\mathrm{evap},i} + a _2 t _{\mathrm{evap},i}^2\right) \end{split} $$

As constantes \(a_j\) podem ser encontradas pelo método dos mínimos quadrados: elas minimizam a soma dos quadrados dos erros.

Felizmente, podemos fazer esses cálculos de minimização com a biblioteca scikit-learn.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

X = t_evap_tc.reshape(-1,1) # para transformar em 2D
Y = m_dot_compressor_tc # 1D

X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2)

m_dot_compressor_model = Pipeline(
[
('poly', PolynomialFeatures(degree=2)),
('linear', LinearRegression(fit_intercept=False))])

# função que faz o ajuste do modelo de fato:
m_dot_compressor_model.fit(X_train, Y_train);

Agora, podemos comparar alguns valores individuais:

i = 20
print("Vazão [kg/s] calculada com modelo físico:")

## Vazão [kg/s] calculada com modelo físico:

print(m_dot_compressor_tc[i])

## 0.010656125541301055

print("Vazão [kg/s] calculada com modelo estatístico:")

## Vazão [kg/s] calculada com modelo estatístico:

print(m_dot_compressor_model.predict([[t_evap_tc[i]]])[0])

## 0.01064898526238194

Vamos ver como o polinômio se sai graficamente:

fig2, ax2 = plt.subplots()
ax2.plot(t_evap_tc,m_dot_compressor_tc*3600,'ko')
ax2.plot(t_evap_tc,m_dot_compressor_model.predict(t_evap_tc.reshape(-1,1))*3600,'k-')
ax2.grid()
ax2.set_xlabel("Temperatura de evaporação [ºC]")
ax2.set_ylabel("Vazão mássica [kg/h]")
plt.show()

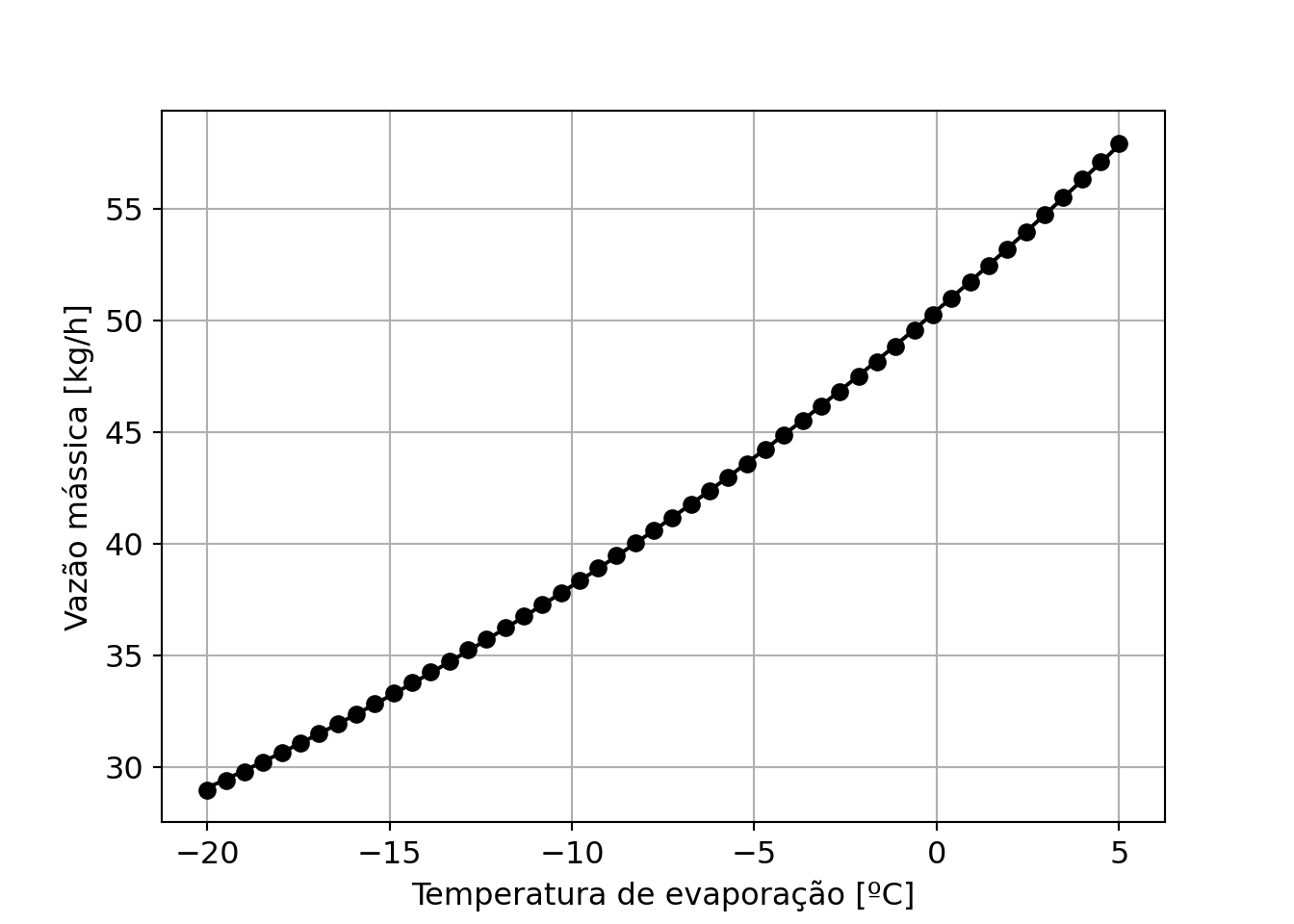Os coeficientes podem ser encontrados:

a_vector = m_dot_compressor_model.named_steps["linear"].coef_
print(a_vector)

## [1.40176573e-02 3.88715386e-04 4.57640783e-06]

Vazão de tubos capilares

Vamos considerar agora um tubo de diâmetro \(D\). A área de escoamento é \(A_{\mathrm{c}}\) O fluido escoa com uma determinada velocidade média mássica \(u_m\):

$$ u_m = \frac{\dot{m}}{\rho A_{\mathrm{c}}} $$

onde, por enquanto, vamos assumir que a densidade é constante.

O escoamento de um fluido através de um tubo de comprimento \(L\) gera uma perda de carga \(\Delta P = P_{\mathrm{cond}} - P_{\mathrm{evap}}\):

$$ \Delta P = f \frac{L}{D} \frac{\rho u_m^2}{2} $$

onde \(f\) é o fator de atrito de Darcy, que depende do número de Reynolds.

Como uma primeira aproximação, vamos considerar um valor constante do fator de atrito. Se os outros parâmetros forem dados, a vazão de um tubo capilar pode ser encontrada como:

$$ \begin{split} \dot{m} & = \rho u_m A_c \\ & = \sqrt{2 \rho \Delta P \frac{1}{f} \frac{D}{L}}A_{\mathrm{c}} \end{split} $$

Se estipularmos um valor de \(f\), e assumirmos o escoamento apenas do líquido saturado pelo tubo, então:

$$ \dot{m} _{\mathrm{capilar}} = \sqrt{2 \rho _l(t _{\mathrm{cond}}) \left(P _{\mathrm{sat}}(t _{\mathrm{cond}}) - P _{\mathrm{sat}}(t _{\mathrm{evap}})\right) \frac{1}{f} \frac{D}{L}}A _{\mathrm{c}} $$

Ou seja: a vazão do tubo capilar de geometria fixa e fator de atrito fixo depende apenas das temperaturas de condensação e evaporação - assim como no compressor.

import math

f = 0.01
D = 1.3e-3
L = 5
Ac = 0.25*math.pi*D**2

def m_dot_tube_fun(t_evap,t_cond):
  P_evap = PropsSI("P","T",t_evap+273,"Q",1,fluid)
  P_cond = PropsSI("P","T",t_cond+273,"Q",1,fluid)
  rhol = PropsSI("D","P",P_cond,"Q",0,fluid)
  DeltaP = P_cond - P_evap
  m_dot_tube = math.sqrt(2*rhol*DeltaP*(1/f)*(D/L))*Ac
  
  return m_dot_tube

m_dot_tube_tc = np.array([
  m_dot_tube_fun(t_evap,t_cond) for t_evap in t_evap_tc
])

fig3, ax3 = plt.subplots()
ax3.plot(t_evap_tc,m_dot_tube_tc*3600,'ko')
ax3.grid()
ax3.set_xlabel("Temperatura de evaporação [ºC]")
ax3.set_ylabel("Vazão mássica [kg/h]")
plt.show()

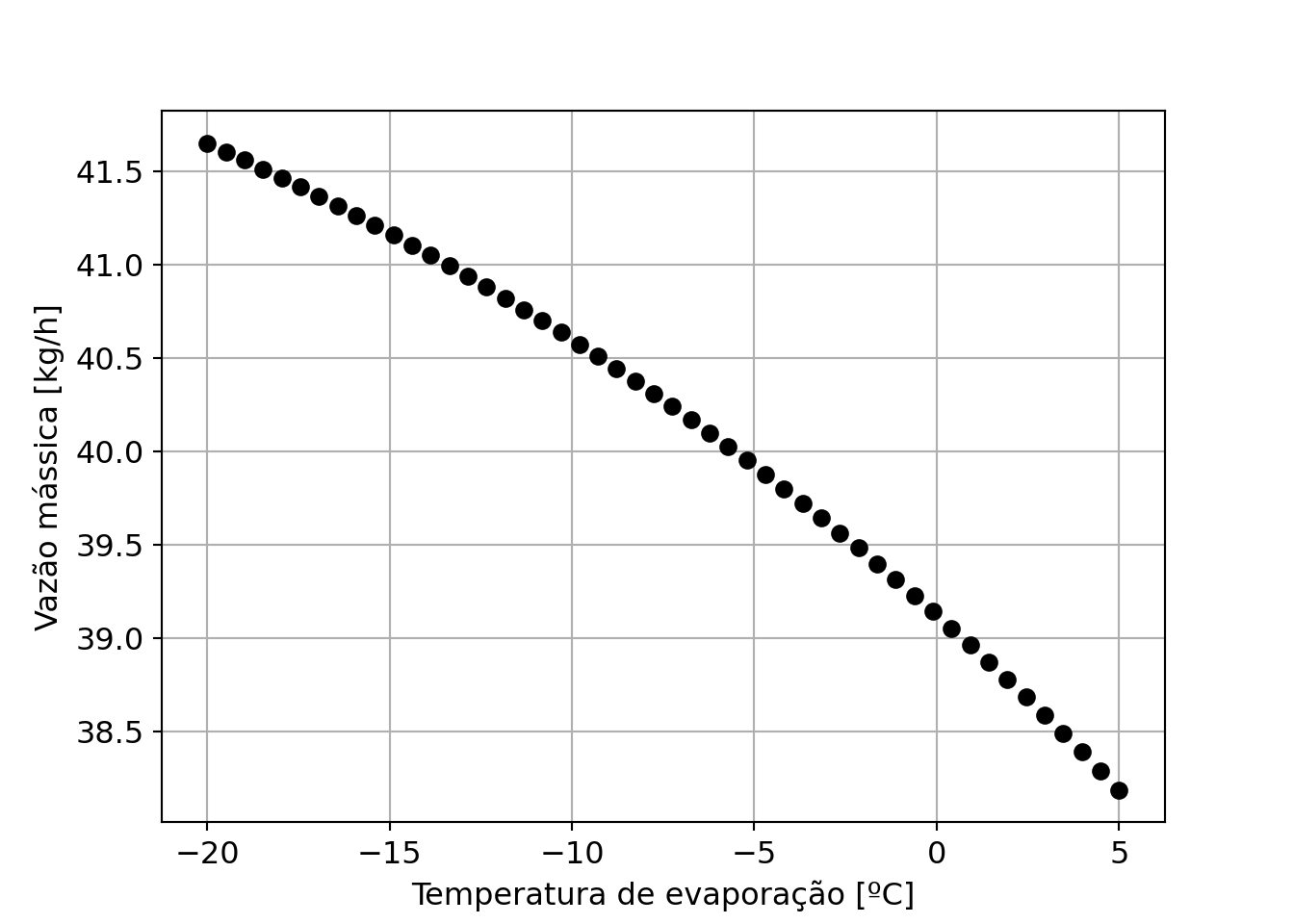
Para pensar : por que o comportamento é inverso ao do compressor?

Ajuste polinomial na vazão de tubos

Repetindo a análise de compressores, podemos tentar ajustar uma curva quadrática a este comportamento:

$$ \dot{m} _{\mathrm{tubo}} = b _0 + b _1 t _{\mathrm{evap}} + b _2 t _{\mathrm{evap}}^2 $$

Y_tube = m_dot_tube_tc # 1D

# cuidado que os valores abaixo vão ser 
# sobre-escritos
X_train,X_test,Y_train,Y_test = train_test_split(X,Y_tube,test_size=0.2)

m_dot_tube_model = Pipeline(
[
('poly', PolynomialFeatures(degree=2)),
('linear', LinearRegression(fit_intercept=False))])

# função que faz o ajuste do modelo de fato:
m_dot_tube_model.fit(X_train, Y_train);

fig4, ax4 = plt.subplots()
ax4.plot(t_evap_tc,m_dot_tube_tc*3600,'ko')
ax4.plot(t_evap_tc,m_dot_tube_model.predict(t_evap_tc.reshape(-1,1))*3600,'k-')
ax4.grid()
ax4.set_xlabel("Temperatura de evaporação [ºC]")
ax4.set_ylabel("Vazão mássica [kg/h]")
plt.show()

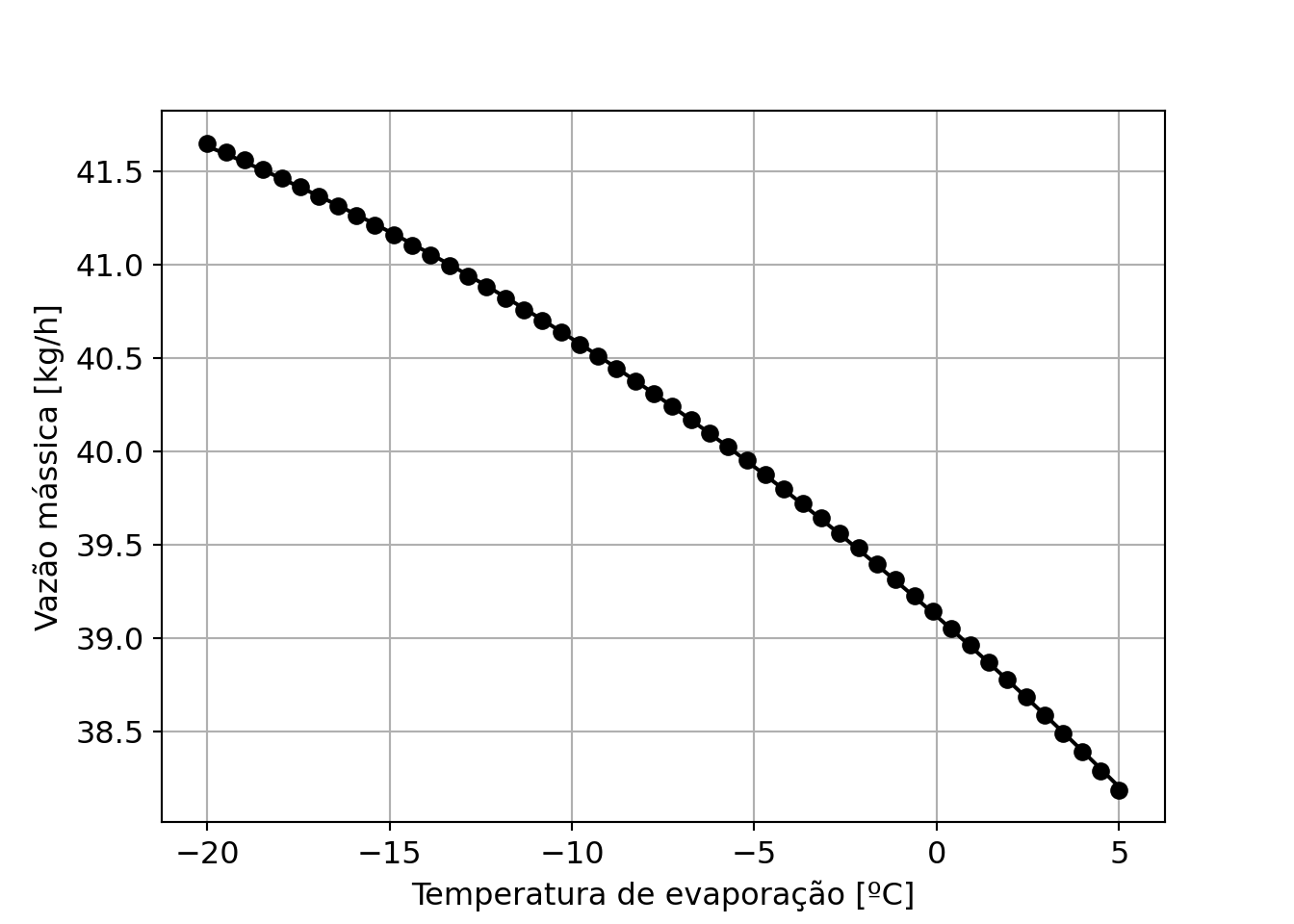Com coeficientes:

b_vector = m_dot_tube_model.named_steps["linear"].coef_
print(b_vector)

## [ 1.08662226e-02 -4.76459272e-05 -6.33742313e-07]

Equilíbrio de curvas

Agora que temos modelos polinomials, podemos manipulá-los mais facilmente. Por exemplo, vamos plotar no mesmo gráfico as duas curvas:

fig5, ax5 = plt.subplots()
ax5.plot(t_evap_tc,m_dot_tube_model.predict(t_evap_tc.reshape(-1,1))*3600,'k-',label="Tubo")
ax5.plot(t_evap_tc,m_dot_compressor_model.predict(t_evap_tc.reshape(-1,1))*3600,'k--',label="Compressor")
ax5.grid()
ax5.set_xlabel("Temperatura de evaporação [ºC]")
ax5.set_ylabel("Vazão mássica [kg/h]")
ax5.legend()
plt.show()

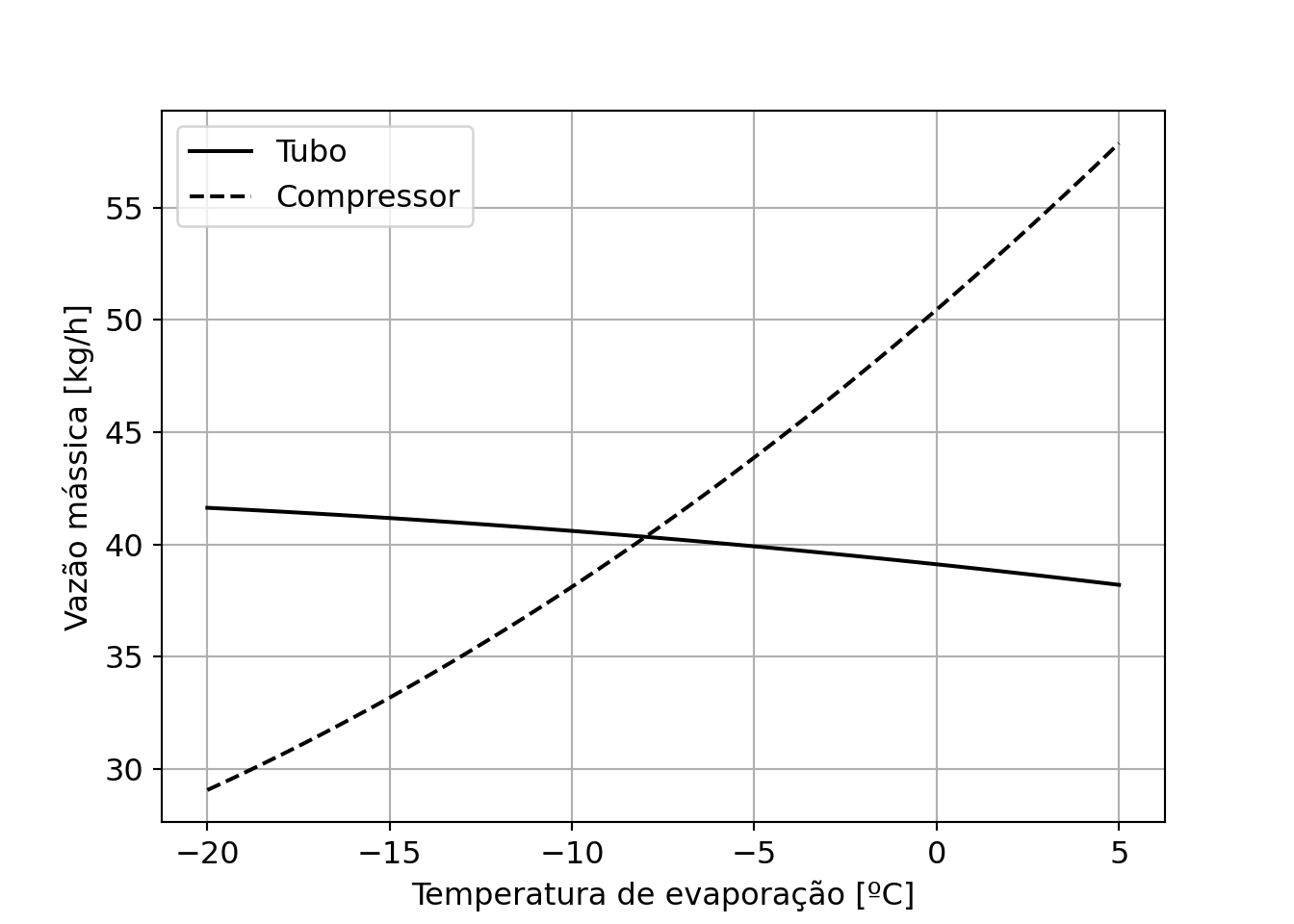
Neste momento, reflita novamente sobre todas as hipóteses levantadas até aqui. O que significa essa interseção dessa curva?

Sugestões de análises futuras:

Modifique os modelos de regressão acima para permitir que a vazão do compressor e do tubo capilar sejam funções da temperatura de evaporação e da temperatura de condensação. Dada uma temperatura de condensação, como você pode encontrar a temperatura de evaporação de equilíbrio? E agora, se a temperatura de evaporação muda, qual vai ser a nova temperatura de condensação?

Calcule também como, ao variar a temperatura de condensação, a temperatura de evaporação de equilíbrio e a vazão de equilíbrio mudam.

Escoamento compressível

A principal limitação era a hipótese de que o escoamento era incompressível, e pegamos então propriedades médias e uma velocidade média ao longo de todo o tubo. Não é isto que acontece em um tubo capilar: a alta perda de carga devido ao pequeno diâmetro abaixa a pressão do fluido, que então consegue evaporar com mais facilidade; o vapor tem menos densidade e portanto consegue escoar com mais velocidade. O fluido acelera ao longo de um tubo capilar; portanto, o nosso modelo de tubo capilar iso-entálpico é falso, uma vez que a entalpia é convertida em energia cinética. Entretanto, é prática ignorar isso como um fator de segurança no projeto de evaporadores; ao assumir que a entalpia não diminui, estamos subestimando o efeito refrigerante no evaporador, e podemos fazer um projeto mais confiável.

Modelo de tubo capilar adiabático

Como as propriedades do fluido (decorrentes da mudança de fase) mudam o tempo todo, precisamos dividir o tubo de comprimento \(L\) e diâmetro \(D\) em pequenos elementos de comprimento \(\Delta L\):

Em regime permanente, a vazão \(\dot{m}\) não muda, e consideramos que a área de seção transversal \(A\) também não. Portanto a razão \(\frac{\dot{m}}{A}\) é uma constante.

No nosso modelo diferencial, as propriedades do estado 1 são sempre conhecidas. Por exemplo, no início do tubo capilar, o estado 1 equivale à saída do condensador, que pode ser de líquido saturado ou sub-resfriado. De qualquer maneira, o volume específico \(v_1\) sempre pode ser determinado. A velocidade na seção 1 é então:

$$ V_ 1 = v_ 1 \frac{\dot{m}}{A} $$

A conservação da massa requer então:

$$ \frac{\dot{m}}{A} = \frac{V_1}{v_1} = \frac{V_2}{v_2} $$

E a conservação da energia (considerando o tubo adiabático, sem realização de trabalho e sem variações de energia potencial) é:

$$ h_1 + \frac{V_1^2}{2} = h_2 + \frac{V_2^2}{2} $$

onde aqui é bem fácil se confundir com as unidades: se a velocidade está em m/s, a entalpia deve estar em J/kg (e não em kJ/kg como é usual).

Que forças agem sobre esse escoamento? O gradiente de pressão \(P_1-P_2\) age no sentido de 1 para 2, enquanto que a força de atrito tenta frear esse movimento. A resultante desse efeito altera a quantidade de movimento de 1 para 2 (já que, ao contrário do modelo da semana passada, a velocidade está mudando agora):

$$ (P _1-P _2) - f _m \frac{\Delta L}{D}\frac{V _m^2}{2v _m} = \frac{\dot{m}}{A}\left(V _2-V _1\right) $$ onde o índice \(m\) se refere a um valor médio no elemento, que assumimos como pequeno para que isso faça sentido.

O fator de atrito local de um escoamento bifásico, com uma incerteza razoável, pode ser estimado como [3]:

$$ f = \frac{0.33}{\mathrm{Re}^{0.25}} $$

Exercício

DESAFIO: criar um algoritmo que permita calcular o comprimento necessário para um tubo capilar de determinado diâmetro. Considere uma condição de entrada conhecida (e.g. líquido saturado na pressão de condensação), uma pressão de saída conhecida, e assuma que o fluido está bifásico o tempo todo. Considere passos de temperatura até atingir a temperatura de evaporação, calcule o comprimento de cada passo e some os valores de todos os passos.

Dica: assuma que as propriedades de saturação (pressão, densidade, viscosidade, entalpia do líquido e do vapor saturado) são conhecidas a cada temperatura.

Blocagem

Se você implementar o algoritmo acima, vai perceber que os comprimentos necessários nos últimos estágios vão se tornando cada vez menores e eventualmente podem ficar negativos. O que está acontecendo?

O escoamento em um tubo capilar é adiabático porém irreversível - portanto, a entropia só pode aumentar. Porém, como a temperatura está abaixando, esse aumento em relação ao estado inicial vai diminuindo; quando ele tentar ser negativo, o escoamento não é mais fisicamente possível. Isso acontece quando o fluido atinge a velocidade do som.

Em um tubo de seção constante, a velocidade do som só pode ocorrer na saída do tubo; não é possível acelerar um fluido hipersônico sem aumentar a área [4]. Portanto, depois que a pressão de saída é tal que a velocidade do som é atingida, diminuir ainda mais a pressão não aumenta a vazão:

Dimensionamento de tubos capilares blocados

O modelo descrito acima é uma primeira estimativa de comprimento necessário, e pode servir de análise de sensibilidade quanto ao diâmetro dos tubos e às pressões de evaporação e condensação. Porém, se a diferença de pressão é grande o suficiente para assegurar a blocagem, então o tubo capilar pode ser dimensionado de maneira mais prática:

Examine o catálogo descrito no vídeo acima; observe cada par (comprimento,diâmetro) é prescrito para uma faixa de temperaturas de evaporação, porque nessas condições é garantido que o escoamento será blocado.

Veja também outro vídeo sobre seleção de tubos capilares:

Esses softwares e catálogos se baseiam em dados experimentais; entretanto, podem ser necessários alguns ajustes, cortando o tubo, até atingir as pressões necessárias.

Referências:

Referências:

[1]: Bergman, T. L., Lavine, A. S., Incropera, F. P., & Dewitt, D. P. Fundamentos da Transferência de Calor e de Massa (7 ed.). Rio de Janeiro: LTC, 2014.

[2]: Bejan, A. Entropy generation minimization: the method of thermodynamic optimization of finite-size systems and finite-time processes. Boca Raton: CRC Press, 1996.

[3]: Stoecker, W. F., & Jones, J. W. Refrigeração e Ar Condicionado. São Paulo: McGraw-Hill do Brasil, 1985.

[4]: Çengel, Y. A., & Boles, M. A. Termodinâmica (7 ed.). Porto Alegre: AMGH, 2013.